去年在学习AP TI-84/NSPIRE艺术统计时,总有一些骚操作让人一头雾水。而每当询问Mr. Z时,他也只是会说“This is an AP level course. You only need to know how to press the calculator”。本篇文章讨论了几个AP统计中涵盖的公式及知识点背后的原理。
Sample Variance Formula
在学习sample variance的时候,我对于其计算公式
s x 2 = 1 n − 1 ∑ ( x i − x ˉ ) 2 s_x^2=\frac{1}{n-1}\sum{(x_i-\bar{x})^2} s x 2 = n − 1 1 ∑ ( x i − x ˉ ) 2 中的n − 1 n-1 n − 1 n n n The Basic Practice of Statistics for AP 431页单纯通过举例子计算的解释显然是一点帮助也没有。。。不过其提到的一个词biased estimator 却的确是问题的关键:
当我们有一个参数为实数θ \theta θ u u u X X X
E [ u ( X 1 , X 2 , … , X n ) ] = θ E[u(X_1,X_2,\ldots,X_n)]=\theta E [ u ( X 1 , X 2 , … , X n ) ] = θ 则我们称 u ( X 1 , X 2 , … , X n ) u(X_1,X_2,\ldots,X_n) u ( X 1 , X 2 , … , X n ) θ \theta θ unbiased estimator 。否则,u ( X 1 , X 2 , … , X n ) u(X_1,X_2,\ldots,X_n) u ( X 1 , X 2 , … , X n ) θ \theta θ biased estimator
对于任意一个服从分布F F F X X X X X X μ \mu μ X X X F F F
V a r ( X ) = σ 2 = E [ ( X − μ ) 2 ] Var(X) = \sigma^2=E[(X-\mu)^2] V a r ( X ) = σ 2 = E [ ( X − μ ) 2 ] 由此可得
V a r ( X ) = σ 2 = E [ 1 n ∑ i = 1 n ( X i − μ ) 2 ] \displaystyle Var(X)=\sigma^2=E[\frac{1}{n}\sum_{i=1}^{n}(X_i - \mu)^2] V a r ( X ) = σ 2 = E [ n 1 i = 1 ∑ n ( X i − μ ) 2 ] 这一个E [ 1 n ∑ i = 1 n ( X i − μ ) 2 ] E[\frac{1}{n}\sum_{i=1}^{n}(X_i - \mu)^2] E [ n 1 ∑ i = 1 n ( X i − μ ) 2 ] unbiased estimator 。而在计算sample variance中,当直接以n n n V a r ( X ) Var(X) V a r ( X ) biased estimator ,并不是我们真正想要的方差。这是因为我们在计算时并不知道X X X μ \mu μ X ˉ \bar{X} X ˉ X ˉ \bar{X} X ˉ μ \mu μ ordinary least squares ,本篇文章不对此进行深入展开)。若以n n n s x ′ 2 s_x^{'2} s x ′ 2
E [ s x ′ 2 ] = E [ 1 n ∑ i = 1 n ( X i − X ˉ ) 2 ] = E [ 1 n ∑ i = 1 n ( X i − μ + μ − X ˉ ) 2 ] = E [ 1 n ∑ i = 1 n ( X i − μ − ( X ˉ − μ ) ) 2 ] = E [ 1 n ∑ i = 1 n ( ( X i − μ ) 2 − 2 ( X i − μ ) ( X ˉ − μ ) + ( X ˉ − μ ) 2 ) ) ] = E [ 1 n ( ∑ i = 1 n ( X i − μ ) 2 − 2 n ( X ˉ − μ ) ( X ˉ − μ ) + n ( X ˉ − μ ) 2 ) ] = E [ 1 n ∑ i = 1 n ( X i − μ ) 2 ] − E [ 1 n ∗ n ( X ˉ − μ ) 2 ] = 1 n E [ ∑ i = 1 n ( X i − μ ) 2 ] − 1 n ∗ n E [ ( X ˉ − μ ) 2 ] = 1 n ( n V a r ( X ) − n V a r ( X ˉ ) ) = V a r ( X ) − V a r ( X ˉ ) \begin{aligned}
E[s_x^{'2}] &= E[\frac{1}{n}\sum_{i=1}^{n}(X_i - \bar{X})^2]\\\\
&= E[\frac{1}{n}\sum_{i=1}^{n}(X_i - \mu + \mu - \bar{X})^2]\\\\
&= E[\frac{1}{n}\sum_{i=1}^{n}(X_i - \mu - (\bar{X} - \mu))^2]\\\\
&= E[\frac{1}{n}\sum_{i=1}^{n}((X_i - \mu)^2 - 2(X_i - \mu)(\bar{X}-\mu) + (\bar{X}-\mu)^2))]\\\\
&= E[\frac{1}{n}(\sum_{i=1}^{n}(X_i - \mu)^2 - 2n(\bar{X} - \mu)(\bar{X}-\mu) + n(\bar{X}-\mu)^2)]\\\\
&= E[\frac{1}{n}\sum_{i=1}^{n}(X_i - \mu)^2] - E[\frac{1}{n}*n(\bar{X}-\mu)^2]\\\\
&= \frac{1}{n}E[\sum_{i=1}^{n}(X_i - \mu)^2] - \frac{1}{n}*nE[(\bar{X}-\mu)^2]\\\\
&= \frac{1}{n}(nVar(X) - nVar(\bar{X}))\\\\
&= Var(X) - Var(\bar{X})
\end{aligned} E [ s x ′ 2 ] = E [ n 1 i = 1 ∑ n ( X i − X ˉ ) 2 ] = E [ n 1 i = 1 ∑ n ( X i − μ + μ − X ˉ ) 2 ] = E [ n 1 i = 1 ∑ n ( X i − μ − ( X ˉ − μ ) ) 2 ] = E [ n 1 i = 1 ∑ n ( ( X i − μ ) 2 − 2 ( X i − μ ) ( X ˉ − μ ) + ( X ˉ − μ ) 2 ) ) ] = E [ n 1 ( i = 1 ∑ n ( X i − μ ) 2 − 2 n ( X ˉ − μ ) ( X ˉ − μ ) + n ( X ˉ − μ ) 2 ) ] = E [ n 1 i = 1 ∑ n ( X i − μ ) 2 ] − E [ n 1 ∗ n ( X ˉ − μ ) 2 ] = n 1 E [ i = 1 ∑ n ( X i − μ ) 2 ] − n 1 ∗ n E [ ( X ˉ − μ ) 2 ] = n 1 ( n V a r ( X ) − n V a r ( X ˉ ) ) = V a r ( X ) − V a r ( X ˉ ) 而sample mean的方差为σ M 2 = σ 2 n \sigma_M^2=\frac{\sigma^2}{n} σ M 2 = n σ 2 X ˉ \bar{X} X ˉ
E [ s x ′ 2 ] = σ 2 − σ 2 n = ( n − 1 ) σ 2 n E[s_x^{'2}]=\sigma^2-\frac{\sigma^2}{n}=\frac{(n-1)\sigma^2}{n} E [ s x ′ 2 ] = σ 2 − n σ 2 = n ( n − 1 ) σ 2 由此可得,当分母为n n n biased estimator ,而将分母变回n − 1 n-1 n − 1 s x 2 s_x^2 s x 2
E [ s x 2 ] = 1 n − 1 ( n V a r ( X ) − n V a r ( X ˉ ) ) = n n − 1 ( n − 1 ) σ 2 n = σ 2 E[s_x^2]=\frac{1}{n-1}(nVar(X) - nVar(\bar{X}))=\frac{n}{n-1}\frac{(n-1)\sigma^2}{n}=\sigma^2 E [ s x 2 ] = n − 1 1 ( n V a r ( X ) − n V a r ( X ˉ ) ) = n − 1 n n ( n − 1 ) σ 2 = σ 2 所以s x 2 = 1 n − 1 ∑ ( x i − x ˉ ) 2 s_x^2=\frac{1}{n-1}\sum{(x_i-\bar{x})^2} s x 2 = n − 1 1 ∑ ( x i − x ˉ ) 2 unbiased estimator 。将原来的biased 的E [ s x ′ 2 ] E[s_x^{'2}] E [ s x ′ 2 ] unbiased 的E [ s x 2 ] E[s_x^2] E [ s x 2 ] n n − 1 \frac{n}{n-1} n − 1 n Bessel’s correction 。
Control of Type II Error
做过AP统计significance test这一章选择题的各位都知道,如果想要减小假设检验发生Type II error (when it fails to reject a null hypothesis H 0 H_0 H 0 z test 中通过增大样本容量降低Type II error发生概率的解释。
Explanation I
第一个解释比较直观。举一个简单例子,现在要估算HFI学生在上一次统计考试中的平均成绩,我们的null hypothesis (H 0 H_0 H 0 μ 1 \mu_1 μ 1 N ( μ 1 , σ 2 ) N(\mu_1, \sigma^2) N ( μ 1 , σ 2 ) H 1 H_1 H 1 μ 1 \mu_1 μ 1 μ 2 \mu_2 μ 2 N ( μ 2 , σ 2 ) N(\mu_2, \sigma^2) N ( μ 2 , σ 2 )
当我们随机选取n n n X ˉ \bar{X} X ˉ z = X ˉ − μ 1 σ / n z = \frac{\bar{X}-\mu_1}{\sigma/\sqrt{n}} z = σ / n X ˉ − μ 1 z score 与对应的P-value ,即可根据P-value 推断学生的平均成绩是μ 1 \mu_1 μ 1 μ 2 \mu_2 μ 2 H 0 H_0 H 0 z score 的计算公式可以得知,X ˉ \bar{X} X ˉ N ( μ 1 , σ 2 n ) N(\mu_1, \frac{\sigma^2}{n}) N ( μ 1 , n σ 2 ) N ( μ 2 , σ 2 n ) N(\mu_2, \frac{\sigma^2}{n}) N ( μ 2 , n σ 2 )
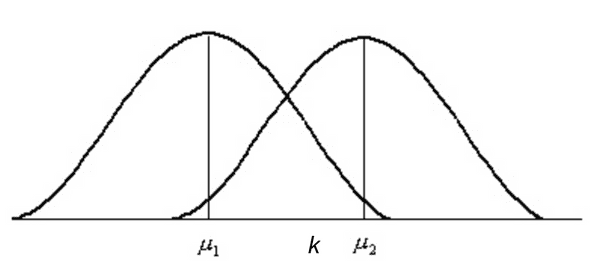
因此,若在下图中x轴上α \alpha α z score 处有一点k k k X ˉ < k \bar{X}< k X ˉ < k H 0 H_0 H 0 X ˉ > k \bar{X}>k X ˉ > k H 0 H_0 H 0
这个时候可得Type II error的概率就是P ( N ( μ 2 , σ 2 n ) < k ) P(N(\mu_2,\frac{\sigma^2}{n})<k) P ( N ( μ 2 , n σ 2 ) < k ) N ( μ 2 , σ 2 n ) N(\mu_2, \frac{\sigma^2}{n}) N ( μ 2 , n σ 2 ) n n n σ 2 n \frac{\sigma^2}{n} n σ 2 μ 1 \mu_1 μ 1 μ 2 \mu_2 μ 2 μ 1 \mu_1 μ 1 μ 2 \mu_2 μ 2 z score 代表的k k k P ( N ( μ 2 , σ 2 n ) < k ) P(N(\mu_2,\frac{\sigma^2}{n})<k) P ( N ( μ 2 , n σ 2 ) < k )
这就是一个对于增大本容量降低Type II error发生概率的解释。不过,用观察图像来解释原理实在是不够让人信服,连一个严谨的数学证明都没有。
对于这一样本容量与Type II error发生概率的关系,是否可以通过数学公式证明呢?
既然如此,下面就来看看第二个更为严谨的解释。
Explanation II
若要通过数学证明来解释样本容量与Type II error发生概率的关系,我们需引入施行特征函数:
若C C C θ \theta θ
β ( θ ) = P θ ( 接受 H 0 ) \beta(\theta)=P_\theta(接受H_0) β ( θ ) = P θ ( 接 受 H 0 ) 称为检验法C C C OC 函数
因此,当θ ∈ H 1 \theta \in H_1 θ ∈ H 1 β ( θ ) \beta(\theta) β ( θ ) 1 − β ( θ ) 1 - \beta(\theta) 1 − β ( θ ) H 0 H_0 H 0 1 − β ( θ ) 1 - \beta(\theta) 1 − β ( θ ) C C C power function ,在这里不深入探究。本文主要介绍通过OC 函数来证明增大本容量可以降低Type II error的发生概率。
我们假设有H 0 : μ < μ 0 H_0: \mu < \mu_0 H 0 : μ < μ 0 H 1 : μ > μ 0 H_1:\mu>\mu_0 H 1 : μ > μ 0 H 0 H_0 H 0 H 1 H_1 H 1 one-sided z test 。对此,我们有OC 函数
β ( μ ) = P μ ( 接受 H 0 ) = P μ ( X ˉ − μ 0 σ / n < z α ) = P μ ( X ˉ − μ σ / n < z α − μ − μ 0 σ / n ) \beta(\mu) = P_\mu(接受H_0)=P_\mu(\frac{\bar{X}-\mu_0}{\sigma/\sqrt{n}} < z_\alpha)=P_\mu(\frac{\bar{X}-\mu}{\sigma/\sqrt{n}} < z_\alpha-\frac{\mu-\mu_0}{\sigma/\sqrt{n}}) β ( μ ) = P μ ( 接 受 H 0 ) = P μ ( σ / n X ˉ − μ 0 < z α ) = P μ ( σ / n X ˉ − μ < z α − σ / n μ − μ 0 ) 此处z α z_\alpha z α α \alpha α z score ,而由于X ˉ − μ σ / n \frac{\bar{X}-\mu}{\sigma/\sqrt{n}} σ / n X ˉ − μ X ˉ \bar{X} X ˉ N ( μ , σ 2 n ) N(\mu,\frac{\sigma^2}{n}) N ( μ , n σ 2 ) z score ,可以得到
β ( μ ) = ϕ ( z α − λ ) \beta(\mu)=\phi(z_\alpha - \lambda) β ( μ ) = ϕ ( z α − λ ) λ \lambda λ μ − μ 0 σ / n \frac{\mu-\mu_0}{\sigma/\sqrt{n}} σ / n μ − μ 0 ϕ \phi ϕ N ( μ , σ 2 n ) N(\mu,\frac{\sigma^2}{n}) N ( μ , n σ 2 ) 分布函数(Cumulative Distribution Function, CDF) ,即正态分布概率密度函数(Probability Density Function, PDF)的变上限积分 。因此,我们有
β ( μ ) = ϕ ( z α − λ ) = 1 2 π ∫ − ∞ z α − λ e − x 2 / 2 d x \beta(\mu) =\phi(z_\alpha - \lambda)=\frac{1} {\sqrt{2\pi}}\int_{-\infty}^{z_\alpha - \lambda}e^{-x ^{2}/2}dx β ( μ ) = ϕ ( z α − λ ) = 2 π 1 ∫ − ∞ z α − λ e − x 2 / 2 d x 当β ( μ ) \beta(\mu) β ( μ ) H 1 H_1 H 1 μ > μ 0 \mu>\mu_0 μ > μ 0 μ − μ 0 > 0 \mu-\mu_0>0 μ − μ 0 > 0 n n n μ − μ 0 σ / n \frac{\mu-\mu_0}{\sigma/\sqrt{n}} σ / n μ − μ 0 λ \lambda λ λ \lambda λ n n n 单调递增 。而当λ \lambda λ z α − λ z_\alpha - \lambda z α − λ β ( μ ) \beta(\mu) β ( μ ) λ \lambda λ 单调递减 。由此可证one-sided z test 增大样本容量可以减小Type II error发生的概率。
类似的,对于一个two-sided z test ,若有H 0 : μ = μ 0 H_0: \mu = \mu_0 H 0 : μ = μ 0 H 1 : μ ≠ μ 0 H_1:\mu\neq\mu_0 H 1 : μ = μ 0 OC 函数
β ( μ ) = P μ ( 接受 H 0 ) = P μ ( − z α / 2 < X ˉ − μ 0 σ / n < z α / 2 ) = P μ ( − λ − z α / 2 < X ˉ − μ σ / n < − λ + z α / 2 ) = ϕ ( z α / 2 − λ ) − ϕ ( − z α / 2 − λ ) \begin{aligned}
\beta(\mu) &= P_\mu(接受H_0)\\\\
&= P_\mu(-z_{\alpha/2} < \frac{\bar{X}-\mu_0}{\sigma/\sqrt{n}} < z_{\alpha/2})\\\\
&=P_\mu(-\lambda-z_{\alpha/2} < \frac{\bar{X}-\mu}{\sigma/\sqrt{n}} < -\lambda+z_{\alpha/2})\\\\
&=\phi(z_{\alpha/2}-\lambda)-\phi(-z_{\alpha/2}-\lambda)
\end{aligned} β ( μ ) = P μ ( 接 受 H 0 ) = P μ ( − z α / 2 < σ / n X ˉ − μ 0 < z α / 2 ) = P μ ( − λ − z α / 2 < σ / n X ˉ − μ < − λ + z α / 2 ) = ϕ ( z α / 2 − λ ) − ϕ ( − z α / 2 − λ ) 由正态分布图像的对称性可知ϕ ( − x ) = 1 − ϕ ( x ) \phi(-x)=1-\phi(x) ϕ ( − x ) = 1 − ϕ ( x )
β ( μ ) = ϕ ( z α / 2 − λ ) + ϕ ( z α / 2 + λ ) − 1 \beta(\mu)=\phi(z_{\alpha/2}-\lambda)+\phi(z_{\alpha/2}+\lambda)-1 β ( μ ) = ϕ ( z α / 2 − λ ) + ϕ ( z α / 2 + λ ) − 1 因为此时应该选择接受H 1 H_1 H 1 μ ≠ μ 0 \mu\neq\mu_0 μ = μ 0 z α / 2 z_{\alpha/2} z α / 2 λ = μ − μ 0 σ / n \lambda=\frac{\mu-\mu_0}{\sigma/\sqrt{n}} λ = σ / n μ − μ 0 λ \lambda λ ϕ ( z α / 2 − λ ) \phi(z_{\alpha/2}-\lambda) ϕ ( z α / 2 − λ ) ϕ ( z α / 2 + λ ) \phi(z_{\alpha/2}+\lambda) ϕ ( z α / 2 + λ ) β ( μ ) \beta(\mu) β ( μ ) ∣ λ ∣ |\lambda| ∣ λ ∣ 单调递减 。而∣ λ ∣ |\lambda| ∣ λ ∣ n n n 单调递增 ,由此可证two-sided z test 增大样本容量可以减小Type II error发生的概率。
此外,对于t test 同样可以用相似的方法证明样本容量与Type II error发生概率的关系,不过推导过程更加复杂,本篇文章不作深入探讨。
Mean and Median in a Skewed Distribution
最后这个问题并不是我自己发现的。今年学统计的H同(ju)学(lao)曾问过我统计书上所写的当一个分布skewed to the left 时,均值小于中位数,反之则均值大于中位数的原因,而我当时并无法回答。原来一直以为理所当然,从来没有深究过背后的原理。但直觉总归是不可靠的,我便去做了一些research。
搞笑的是,“skewness ”在历史上正是通过均值与中位数的大小关系定义的。。。
不过现代的“skewness ”已经改用三阶中心矩来定义了。
如果想更多了解这一点,可以去看看这一个知乎回答 。
Conclusion
以上就是对于AP统计中我认为的几个主要的比较有意思的问题背后的原理。
其实在学习HFI数理方面课程的时候,总是给人一种“不求甚解”的感觉,本来应该讲究数学推导,却学成了依靠背诵知识点过关的科目。下到统计,上到AC,无一例外。这对理解这一门学科所学的内容与将来的理科学习是相当不利的。尽管出于自身水平的限制,不能一一钻研自己感兴趣的所有学过而又不理解的知识点,但我始终觉得应当在学习的过程中有一种多问“为什么”的精神:起码这也能让自己学到这门科目的一点皮毛,对得起这真tm贵的学费和AP考试费,而不是在学完之后发现自己仅仅只是学会怎么操作一个工具而已。
希望本文能给广大挣扎在AP统计中的出国党一点帮助,也激励自己和大家对于自己真正喜欢的学科不要仅仅满足于课程考试 虽然不感兴趣的学科我经常这么干(大雾),永远保持一种“好求甚解”的习惯。
References
[1]盛骤, 谢式千, 潘承毅. 概率论与数理统计, 第四版[M]. 高等教育出版社, 2008.